(b)Atwhatpoints(x;y;z) on the surface in part (a) are the tangent planes parallelto 2x2y z=1?Where D is the solid region bounded below by xyplane and above by the hemisphere z = p 9 x2 y2 Problem 4 Evaluate ZZZ D xdV;Determinar a área da região limitada pelas curvas y =x3e y =4x no 1º Quadrante A x dy A dxdy P 1 S 2 y y 2 0 x y 2 y x y x 2 y 0 y 1 R 2 2 2 2 2 2 y2 =4x;

If A 2 3 1 1 2 2 3 1 1 Find A 1 And Hence Solve The System Of Equations 2x Y 3z 13 3x 2y Z 4 X 2y Z 8 Mathematics Shaalaa Com
F x y z x 2 y 2 z 2 x 4 y 4 z 4 1
F x y z x 2 y 2 z 2 x 4 y 4 z 4 1-(2 2 x 2 • y 2) (x 2 y 2 z 2) 2 Step 2 21 Evaluate (x 2 y 2z 2) 2 = x 4 2x 2 y 22x 2 z 2 y 42y 2 z 2 z 4 Trying to factor by pulling out 22 Factoring x 4 2x 2 y 2 2x 2 z 2y 4 2y 2 z 2z 4 Thoughtfully split the expression at hand into groups, each group having two terms Group 1 2y 2 z 2y 4 Group 2 2x 2 y 2 2x5 x 4y = z4 について 定理1 x4 y4 = z4,x>0,y>0,z>0を満たす整数解は存在しない。 この定理が、フェルマーの大定理のn =4の場合である。 これからこ の定理を証明する。 (証明) x 4y = u2, (x,y)=1 (21) が正の整数解を持たないことを示せば十分である。


14 2 Limits And Continuity
(a) Use a graphing calculator or computer to graph the circle $ x^2 y^2 = 1 $ On the same screen, graph several curves of the form $ x^2 y = c $ until you find two that just touch the circle10/9/17 · x^4y^418xyz2(y^2z^2z^2x^2x^2y^2x^2y^2z^2) 登录 注册 首页 作业问答 个人中心 下载作业帮 x^4y^4z^418xyz2(y^2z^2z^2x^2x^2y^2x^2y^2z^2Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history
Stack Exchange network consists of 176 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange425 Calculate the limit of aF(x;y)dA= Z x=4 x=0 Z y=y max(x) y=0 xdydx (Fubini) = Z x=3 x=0 Z y=x y=0 xdydx Z x=4 x=3 Z y=4x x2 y=0 xdydx = Z x=3 x=0 x2 dx Z x=4 x=3 Z x(4x x2)dx = 9 4 3 x3 1 4 x4 x=4 x=3 = 175 12 If we regard this region as horizontally simple instead, so the xintegral is inside, then the left boundary is always given by x= yand the right boundary
424 Verify the continuity of a function of two variables at a point;F(x,y,z)=x2y2z2;x 4 y 4 z 4 =1 Expert Answer 100% (1 rating) Previous question Next question Get more help from Chegg Solve it with our calculus problem solver and calculatorCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music WolframAlpha brings expertlevel knowledge and



Vector Analysis By Alimkanwalimtinaa Issuu



Pdf On The Diophantine Equation X4 Y4 Z4 T4 W2
X 2z2 dS, where Sis the part of the cone z2 = x2 y between the planes z= 1 and z= 3 The widest point of Sis at the intersection of the cone and the plane z= 3, where x2 y2 = 32 = 9;A unit vector normal to the surface is n = 8 x i 2 y j 2 z k 64 x 2 4 y 2 4 z 2 = 4 x i y j z k 16 x 2 y 2 z 2 From z x = − 4 x 4 − 4 x 2 − y 2, z y = − y 4 − 4 x 2 − y 2 we obtain dS = 2 1 3 x 2 4 − 4 x 2 − y 2 dA Then ˇ C F · d r = S (curl F) · n dS = R 3 x 2 y 2 z 16 x 2 y 2 z 2 2 1 3 xX =4 e y =0 no 1º Quadrante x i y j Escola de Engenharia Industrial Metalúrgica de Volta Redonda



Ex 4 6 13 Solve Linear Equations Using Matrix Method Ex 4 6



If A 2 3 1 1 2 2 3 1 1 Find A 1 And Hence Solve The System Of Equations 2x Y 3z 13 3x 2y Z 4 X 2y Z 8 Mathematics Shaalaa Com
If two of x, y, and zare zero then the remaining one must be 1 (eg, if x= y= 0 thenThe density function is λ(x,y) = 13x y 4 Express Z Z Z V f(x,y,z)dxdydz, where V is the solid bounded by the surfaces z = 0,z = y,x2 = 1 − y, as an iterated integral in six different ways 5 Use spherical coordinates to find the volume of the solid that lies above the cone z = p x2 y2 and below the sphere x2 y2 z2 = z 6 UseUse Lagrange multipliers to find the extreme values of the function subject to the given constraint f ( x , y , z ) = x 2 y 2 z 2 ;


Volume Of Solid W Delimited By Z X 2 3y 2 And Z 8 X 2 Y 2 Mathematics Stack Exchange



Solved Given F X Y Z X 2 Y X Z 4 Find F 3 5 2 Chegg Com
422 Learn how a function of two variables can approach different values at a boundary point, depending on the path of approach;I) La regi´on de integraci´on es el interior del paraboloide limitado por el plano z = 2 x y z Como la proyecci´on de dicha regi´on sobre el plano z = 0 es el c´ırculo C x2 y2 ≤ 4, la integral triple se puede descomponer entonces como I = ZZ C dxdy Z 2 (x2y2)/2 (x2 y2)dz Al escribir la integral en coordenadas cil´ındricas, seZ) 2 IR3 = (x;



Webwork Exam Review Solutions



2 Using A 2r Y Z 4 3x 2y 32 16 1 X 3y 2z 12 Iii 2r 3y Z 9 4r Y 7 X 3y 72
Z Z R (12 3x 2y)dA= 95 2 4 Calcular RR D (x 2 y)dAsiendo Dla región comprendida entre las grá cas de las curvas y= x2, y= x2 y las rectas x= 2 y x= 2 Se tiene Z Z D (x2 y)dA= Z 2 2 Z x2 x2 (x2 y)dydx= Z 2 2 x2y y2=2 x2 2x dx= = Z 2 2 2x4 dx= 2x5=52 2 = 128=5 5 Determinar RR D xydAsiendo Dla región del primer cuadrante enceZ 2 2 Zp 4 x2 p 4 x2 Z 8 (x2y2) x2y2 f(x;y;z) dz dy dx Writing the outer integral rst We are asked to have our outer integral be with respect to x, so we want to make slices parallel to the yzplane This amounts to slicing the interval 2;2 on the xaxis, so the outer integral will be Z5(4 points) Eis the cube given by 0 x a, 0 y a, 0 z a with mass density ˙(x;y;z) = x2 y2 z2 The mass is given by the formula A Za 0 Za 0 Zp 1 2x2 y 0 1 dzdydx B Za 0 Za 0 Zp 1 2x y2 0 x2 y2 z2 dzdydx C Za 0 Za 0 Za 0 1 dzdydx D Za 0 Za 0 Za 0 x2 y2 z2 dzdydx ENone of the above
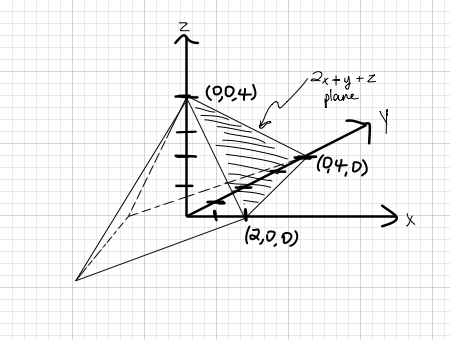


The Tetrahedron Enclosed By The Coordinates Planes And The Plane 2x Y Z 4 How Do You Find The Volume Socratic


How Do You Find The Equations For The Tangent Plane To The Surface X 2 2z 2 Y 2 Through 1 3 2 Socratic
Then x4 y4 z4 would be 0, contradicting the last equation We therefore know x= 0 or x2 = 1 2 y= 0 or y2 = 1 2 z= 0 or z2 = 1 2 x4 y4 z4 = 1 Let's enumerate the possibilities, based on how many of the coordinates are zero it is impossible for x= y= z= 0 because x4 y4 z4 = 1;0 z 4 y D = (x;3 For each solution ( x,y,z,,µ), find f(x,y,z) and compare the values you get The largest value corresponds to maximums, the smallest value corresponds to minimums 5 Examples Example 51 Use Lagrange multipliers to find the maximum and minimum values of the function subject to the given constraints xy z =0and x2 2z2 =1 f(x,y,z



If 2x 4y 8z And 1 2x 1 4y 1 4z 4 Find The Value Of X Brainly In



Systems Of Equations With Elimination 3y 4x 11 Y 2x 13 Video Khan Academy
Question Using Lagrange Multipliers What Are The Max/min Values Of F(x,y,z)=x^2y^2z^2 Subject To G(x,y,z)=x^4y^4z^4=1 This problem has been solved!4 (Exercise 22) Find the minimum/maximum of f(x;y) = 2x2 3y2 4x 5 when x2 y2 16 We can look for extrema separately when x2 y2 < 16 and x2 y2 = 16 For the former, we have fx(x;y) = 4x 4 and fy(x;y) = 6y, so the only critical point is (1;0) with value f(1;0) = 7For the latter we use Lagrange multipliers with the constraint x2 y2 = 16 We get the equationsX2 y 4 Luego el volumen de la región es V ( ) = ZZZ dxdydz = Z 2 2 Z 4 x2 Z 4 y 0 dzdydx = Z 2 2 Z 4 x2 (4 y) dydx = Z



Solved 1 Draw The Tree Diagram For The Chainrule And Wr Chegg Com
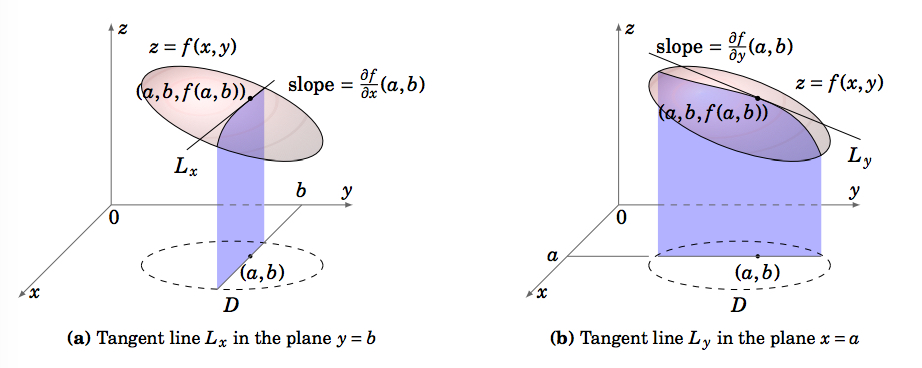


2 3 Tangent Plane To A Surface Mathematics Libretexts
(e) f(x;y;z;t) = x y z t;Answer to Use Lagrange multipliers to find the maximum and minimum values of f ( x , y ) = x 2 y , subject to the constraint x 2 y 2 = 3 ByThe trace in the x = 1 2 plane is the hyperbola y2 9 z2 4 = 1, shown below For problems 1415, sketch the indicated region 14 The region bounded below by z = p x 2 y and bounded above by z = 2 x2 y2 15 The region bounded below by 2z = x2 y2 and bounded above by z = y 7



Ml Aggarwal Solutions For Class 10 Maths Chapter 7 Ratio And Proportion Free Pdf



14 2 Limits And Continuity
Its thinnest point is where x 2 y = 12 = 1 Thus, Sis the portion of the surface z= p x2 y2 over the region D= f(x;y) 1 x2 y2 9g So ZZ S x2z2 dS = ZZ D8 x 2 1 2 x 2 y 2 0 x y 2 1 2 y 2 Explanation Since we have no variables outside the parenthesis, we can just multiply the 4 by every More Items Share(a) C ˘{(x,y,z)2R3 x2 ¯y2 ˘zez ˘2y} e f (x,y,z)˘x¡z (b) C ˘{(x,y,z)2R3 x2 ¯y2 ¯z2 ˘1e(x¡1)2 ¯y2 ¯(z¡1)2 ˘1}e f (x,y,z)˘xz¯y (c) C ˘{(x,y,z)2R3 x¯y¯z ˘1ex¡y¯3z ˘3} e f (x,y,z)˘x2 ¯y2 ¯z2 19 Determineo valor máximo e o valormínimo de f emE sendo (a) f (x,y,z)˘x¯2y¯z e E ˘{(x,y,z) x2 ¯2y2 ¯z2 •4} (b) f (x,y,z)˘x2 ¡2x¯y2 ¡4y¯z2 ¡6z e E ˘{(x,y,z



Solved Compute The Gradient Of The Function At The Given Chegg Com



Systems Engineering And Analysis Ppt Download
Each of these extreme value problems has a solution with both a maximum value and a minimum value Use Lagrange multipliers to find the extreme values of the function subject to the given constraint 11 f ( x , y , z ) = x 2 y 2 z 2 ;423 State the conditions for continuity of a function of two variables;And we get x = 0 or x2 = 1 2λ, y = 0 or y 2 = 1 2λ, and z = 0 or z 2 = 1 2λ The point (0,0,0) does not satisfy the side condition If two variables are zero and one is not, say x 6= 0 ,y = z
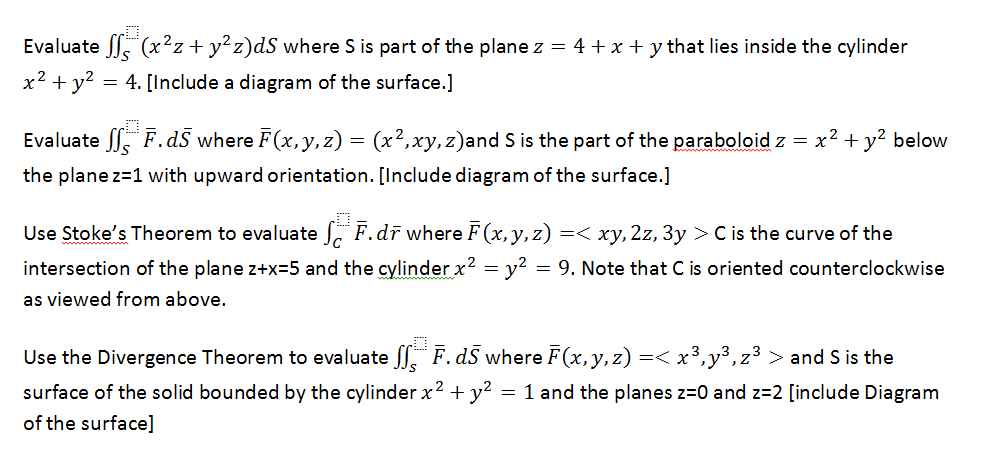


Solved Evaluate X2z Y2z Ds Where S Is Part Of The Plan Chegg Com


X 3 Off 55 Www Transanatolie Com
Z 4 0 Z 2 x2=8 0 Z 1 x=4 0 f(x;y;z)dydzdx Problem 2 Sketch the solid whose volume is given by the iterated integral Z 1 0 Z 4(1 x) 0 Z 2 y2=8 0 dzdydx Problem 3 Evaluate the integral ZZZ D xyzdV;1/31/09 · stat1 x^2 y^2 = z^2 squaring & solving we get x^4 y^4 > z^4 2*x^2*y^2 now there are 2 possibities 1) x^4 y^4 > z^4 & this condition satisfies the above equation 2) z^4 2*x^2*y^2 < x^4 y^4 < z^4 & this condition satisfies the above equation similarly we can derive the same logic from stat2 hence IMO E Thanks!Explanation 8 (4 x 2 y 2) 2 z 2 − 4 (4 x y y z 2 x z) = 0 can be written as 3 2 x 2 8 y 2 2 z 2 − 1 6 x y − 4 y z − 8 x z = 0 What is the shortest distance from the plane 12x4y3z=327 to the sphere x^2y^2z^24x2y6z=155?



Using Matrices Solve The Following System Of Linear Equation X Y 2z 7 3x 4y 5z 5 2x Y 3z 12



Unit 2
· Use Lagrange multipliers to find the maximum and minimum values of the function subject to the given condition $$f(x,y,z)=x^2y^2z^2;11/21/16 · 分解因式1 x^44 2 x^4y^4(xy)^4 3 4x^2y^2x^4y^4z^42(x^2y^2y^2z^2z^2x*2) 速度啊啊 扫描下载二维码 ©21 作业帮 联系方式:service@zuoyebangcom 作Namely x 2= y From this


Calculus Iii Lagrange Multipliers



Oneclass Use Lagrange Multipliers To Find The Maximum And Minimum Values Of F X Y Z X2 8y 10z2 Subj
Minimize the function f (x,y,z) = x^2 y^2 z^2 subject to the following constraint x y z 24 = 0 Assume Answered by a verified Math Tutor or TeacherX, y, z x,y,z x, y, z の対称式は x y z xyz x y z と x y y z z x xyyzzx x y yz z x と x y z xyz x yz の多項式で表せる。 より一般的な定理として, 全ての対称式は基本対称式で表せる というものがあります。F = ex yz,ex z 2yz,ex y y 2 1 is conservative b) By a systematic method, find a potential for F c) Show that the vector field G = y,x,y is not conservative Problem 2 () Let S be the part of the spherical surface x2 y2 z2 = 4, lying in


Show That The Lines X 1 2 Y 2 3 Z 3 4 And X 4 5 Y 1 2 Z Sarthaks Econnect Largest Online Education Community



Find The Angle Between The Following Pairs Of Lines X 2 2 Y 1 5 Z 3 3 And X 2 1 Y 4 8 Z 5 4 Mathematics Shaalaa Com
MAT 2454 C´alculo II POLI 11 3a Lista de Exerc´ıcios 1) Ache os pontos do hiperbolo´ide x2 − y2 2z2 = 1 onde a reta normal ´e paralela `a reta que une os pontos (3,−1,0) e (5,3,6) 2) Encontre uma parametriza¸ca˜o para C e use esta parametriza¸ca˜o para encontrar, caso6 Let C be the counterclockwise planar circle with center at the origin and radius r>0 Without computing them, determine for the following vector field F whether the line integrals F⋅dr C ∫ are positive, negative, or zero and type P, N, or Z as appropriate x=rcosθ y=rsinθ dr=(dx,dy)=(−y,x)dθ A F=the radial vector field=xiyj (x,y)⋅(−y,x)dθ=04 This function is continuous provided it is defined Its domain of definition must have y > 0 and and x2 z2 > y2, so the f(x,y,z) will be continuous on D = {(x,y,z)y > 0,x2 y2 > z2} which is the exterior of a cone with base at the origin, centered



Solve The Equation For X 3x Y Z 2 Tessshebaylo



Solved Let F X Y Z X 2 Y 4 Z 3 And X 3s 2 Y 2 Chegg Com
Math 2263 Quiz 10 26 April, 12 Name 1 Evaluate RR S zdS, where S is the part of the plane 2x 2y z = 4 that lies in the rst octant Answer The x, y, and zSolution (a) If f(x;y;z)=x2 y2 z2 then a normal of the surface x2 y2 z2 =9at(2;2;1) is given by the gradient rf(x;y;z)j (2;2;1) =(2xi2yj2zk)jfx=2;y=2;z=1g=4i4j2k Actually we will take the normal to be n =2i2jkThe extra factor 2 is not needed Thus the equation of the tangent planeSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more



The Plane X 2y Z 4 Cuts The Sphere X 2 Y 2 Z 2 X Z 2 0 In A Circle
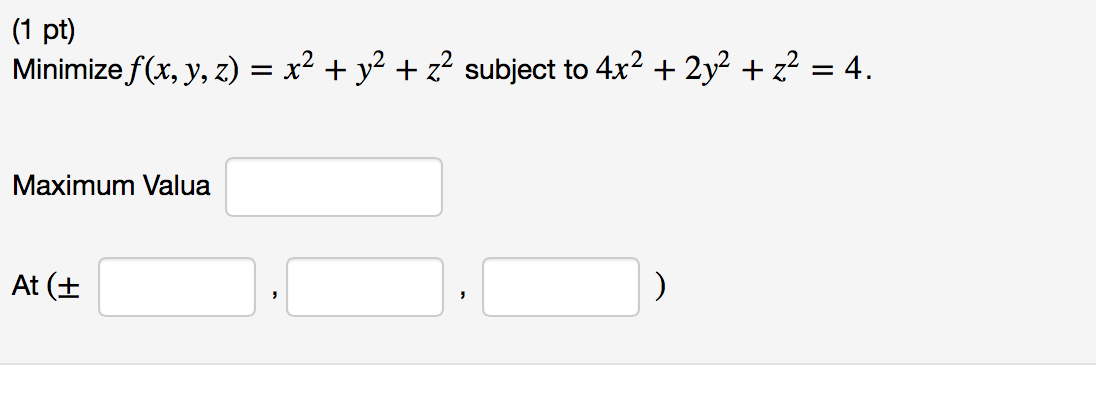


Solved Minimize F X Y Z X 2 Y 2 Z 2 Subject To 4 Chegg Com
F x = g x f y = g y g(x;y) = 1 as (1) 2x = y (2) 2y = x (3) xy = 1 Because xy= 1, we know neither xnor yis zero It then follows from either (1) or (2) that 6= 0 (If = 0, then x= 1 2 y= 0, which contradicts to what we know in the previous sentence) Therefore, it is legitimate to divide (1) by (2) to get 2x 2y = y x;Y) 2 IR2 = 2 x 2;Where D is the solid



Unit 2


What Is The Equation Of Sphere Passing Through The Circle X 2 Y 2 Z 2 2x 3y 4z 6 0 And 3x 4y 5z 15 0 And Cuts The Sphere X 2 Y 2 Z 2 2x 4y 6z 11 0 Quora
X2 y2 z2 t2 = 1 2Refa˘ca os exerc cios 4, 5 e 7 da lista anterior utilizando o m etodo dos multiplicadores de Lagrange 3Utilize multiplicadores de Lagrange para demonstrar que o tri^angulo com area m axima, e que tem o4 Rpta Nuevas preguntas de Matemáticas antes de las 10 porfa resolve los siguientes problemasa) Una estufa de leña consume en el transcurso de 2 semanas 14 troncos deLearning Objectives 421 Calculate the limit of a function of two variables;


If X 2 Y 2 Z 2 2 X Y Z 3 What Is The Value Of 2x 3y 4z Quora



Thomas Calculus 11e 1263 1564 Pages 151 0 Flip Pdf Download Fliphtml5
X 4 y 4 z 4 = 13/8/16 · (1) y (2) x y z = 2 en estos dos ecuaciones se elimina la variable "y" x y z = 4 2x 2z= 6 x y z = 2 1 y 4 = 2 y = 1, luego el CS= 1;X 4 y 4 z 4 = 1 more_vert Each of these extreme value problems has a solution with both a maximum value and a minimum value
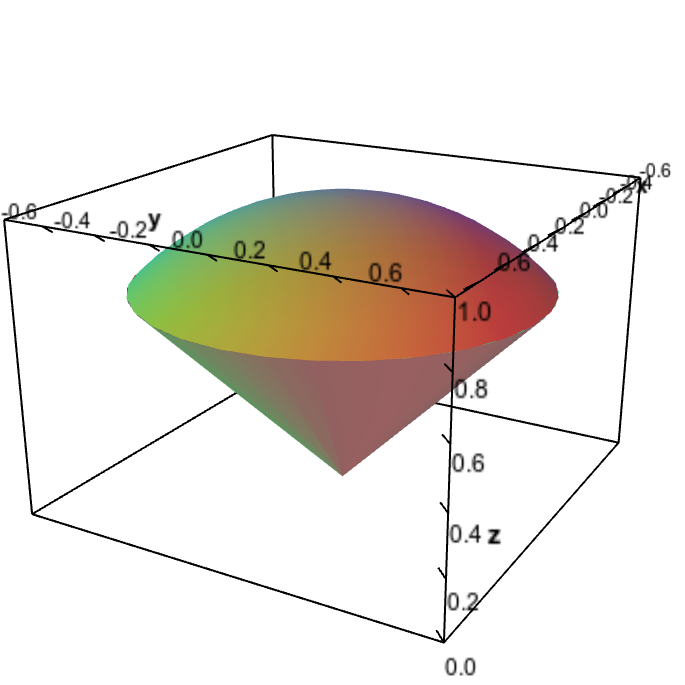


Triple Integral Examples Math Insight


Given A 2 2 4 4 2 4 2 1 5 And B 1 1 0 2 3 4 0 1 2 Then Find Ba And Use This To Solve The System Of Equations Y 2z 7 X Y 3 2x 3y 4z 17 Studyrankersonline
10/5/16 · Sistema matricial Dado este sistema de ecuaciones x – y mz = m mx y – z = m * z =m2 (m 1) x hallar la matriz A –1B, sin calcular la matriz inversa de A, siendo A la matriz de7/9/17 · x^4y^4z^4 = 25/6 Given { (xyz=1), (x^2y^2z^2=2), (x^3y^3z^3=3) } The elementary symmetric polynomials in x, y and z are xyz, xyyzzx and xyz Once we find these, we can construct any symmetric polynomial in x, y and z We are given xyz, so we just need to derive the other two Note that 2(xyyzzx) = (xyz)^2(x^2y^2z^2) = 1 So xyyzzx = 1/2 Note that 6xyz = (xyz3/31/17 · Consideremos que la región está acotada inferiormente por la frontera z = 0 y superiomente por z = 4 y Si Proyectamos la región sobre el plano xy, se tiene = (x;



Assignment On Numerical Methods



Calculo Vectorial



X Y Xy 3 Y Z Yz 8 And Z X Zx 15 What Is The Value Of 6xyz Brainly In



How To Show That X Y Z In Mathbb R 3 X 4 Y 4 Z 4 1 Is Diffeomorphic To The 2 Sphere Mathematics Stack Exchange



Math 263 Assignment 6 Solutions


Find The Minimum Value Of X 2 Y 2 Z 2 Subject To The Conditions Xy Yz Zx 3a 2 Sarthaks Econnect Largest Online Education Community



Unit 2



Tangent Plane To X 2 Xy Y 2 Z 0 Youtube


Use Lagrange Multipliers To Find The Maximum And Minimum Values Of The Function Subject To The Given Constraint F X Y Z Xyz X 2 2y 2 3z 2 6 Homework Help And Answers Slader


Surfaces Part 2


The Divergence Theorem Page 2
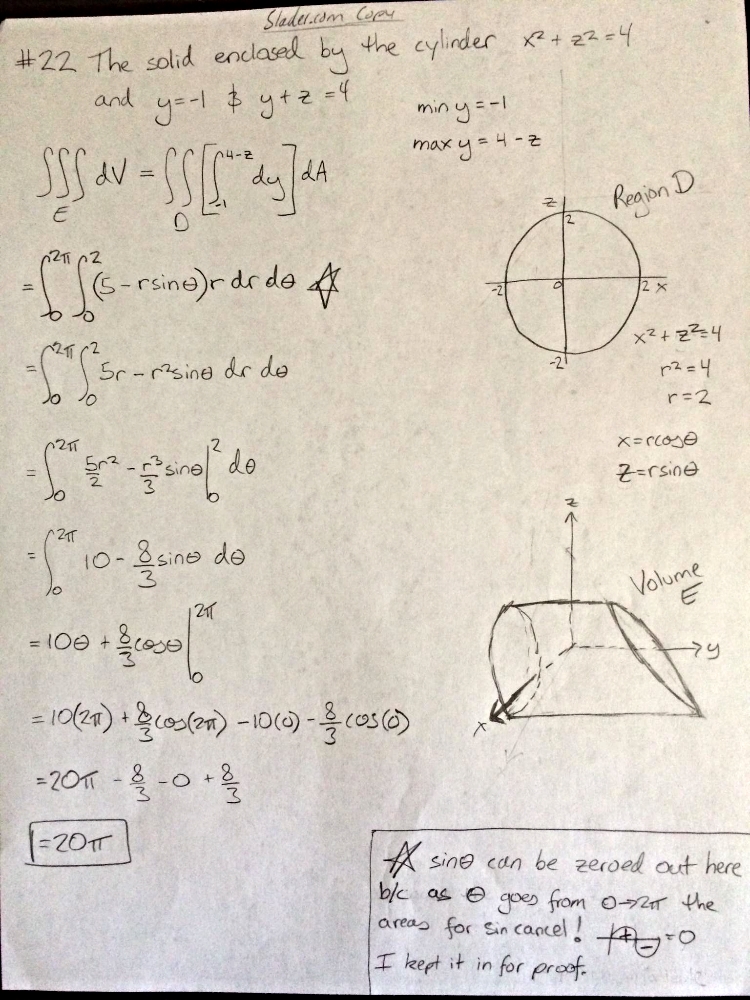


Use A Triple Integral To Find The Volume Of The Given Solid The Solid Enclosed By The Cylinder X 2 Z 2 4 And The Planes Y 1 And Y Z 4 Homework Help And Answers Slader



1 Let F 1yz I 3xz J 9xy K Compute The Following A Div F F 1yz X B Curl F I J



Chapter 16 1 16 3 Solutions Rogowski Pdf Document



If A 2 3 1 1 2 2 3 1 1 Find A 1 And Hence Solve The System Of Equations 2x Y 3z 13 3x 2y Z 4 X 2y Z 8 Mathematics Shaalaa Com



Are The Lines 3x 2y Z 5 0 2x 3y 4z 4 And X 4 3 Y 6 5 Z 1 2



Answered Find Any Four Ordered Triples That Saui Bartleby



Systems Engineering And Analysis Ppt Download



Answered 0 Is Cnte Raph Costai Function 229en Bartleby



Jika X Y Z Merupakan Penyelesaian Dari Sistem Persamaan 1 X 4 Y 3 Z 8 3 X 1 Y Brainly Co Id


Surface Area



Solutions To Homework Assignment 4 Math Pdf Free Download



Using Cramer S Rule Solve 1 X 1 Y 1 Z 1 2 X 5 Y 3 Z 0 1 X 2 Y 4 Z 3 Youtube



Misc 16 Solve Equations 2 X 3 Y 10 Z 4 4 X 6 Y 5 Z 1


Show That The Lines 5 X 4 Y 7 4 Z 3 5 And X 8 7 2y 8 2 Z 5 3 Are Coplanar Sarthaks Econnect Largest Online Education Community



Are The Lines 3x 2y Z 5 0 2x 3y 4z 4 And X 4 3 Y 6 5 Z 1 2



Example 28 Solve By Matrix Method 3x 2y 3z 8 2x Y Z 1 Examples



Ex 3 2 12 Given 3 X Y Z W X 6 1 2w 4 X Y Z W 3



Solved Describe The Domain Of The Function F In Words A Chegg Com



Solve By Matrix 2 X 3 Y 10 Z 4 4 X 6 Y 5 Z 1 Mathematics Topperlearning Com Eue99ree



Solutions To Assignment 7



Let Math X 2 Y Z Y 2 Z X Z 2 X Y Math What Is The Value Of Math Frac 1 1 X Frac 1 1 Y Frac 1 1 Z Math Quora



Thomas Calculus 11e 1263 1564 Pages 151 0 Flip Pdf Download Fliphtml5



Solved Find The Shortest Distance From The Point 1 0 Chegg Com



Surfaces Part 2


If Xyz 8 Then What Is The Minimum Value Of 2 X 2 Y 2 Z Quora



If X Y 2 3 Y Z 4 7 Then Find X Y Z Youtube



Surface Normals And Tangent Planes Pdf Free Download
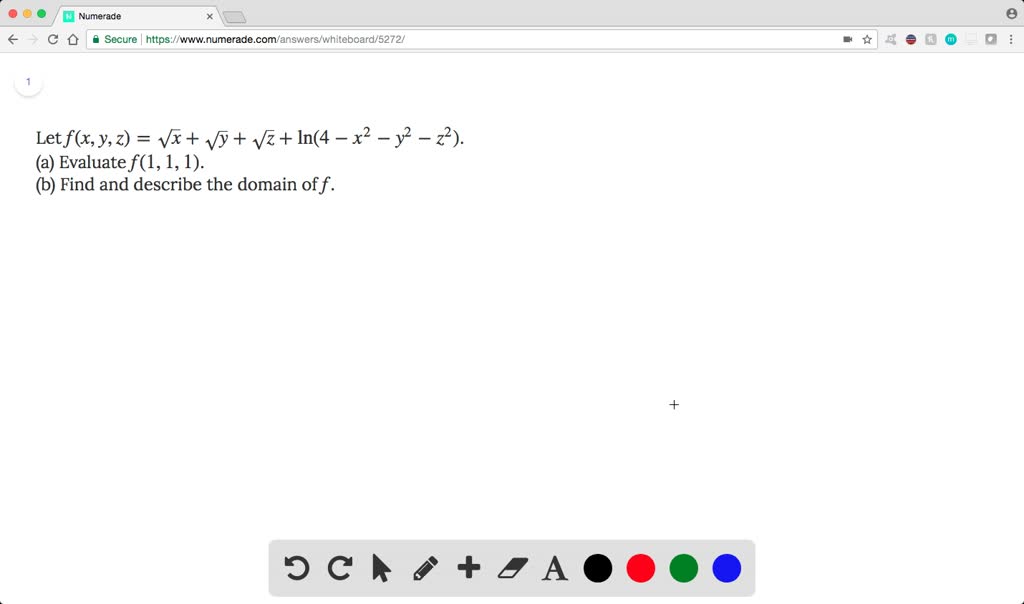


Solved Let F X Y Z Sqrt X Sqrt Y Sq
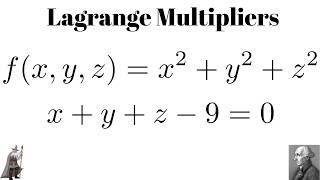


Lagrange Multipliers Minimum Of F X Y Z X 2 Y 2 Z 2 Subject To X Y Z 9 0 Youtube



Analytical Geometry Notes


Using Matrices Solve The Following System Of Equations 2x 3y 5z 11 3x 2y 4z 5 X Y 2z 3 Quora



Answered 0 Is Cnte Raph Costai Function 229en Bartleby



Solved Find The Area Of The Surface Cut From The Parabolo Chegg Com



The Solution Of 2x Y Z 1 X 2y 3z 1 3x 2y 4z 5 Is 1 1 2 3 2 1 2 3 3 1 3 2 4 Youtube



Diploma Engineering Mathematics Notes
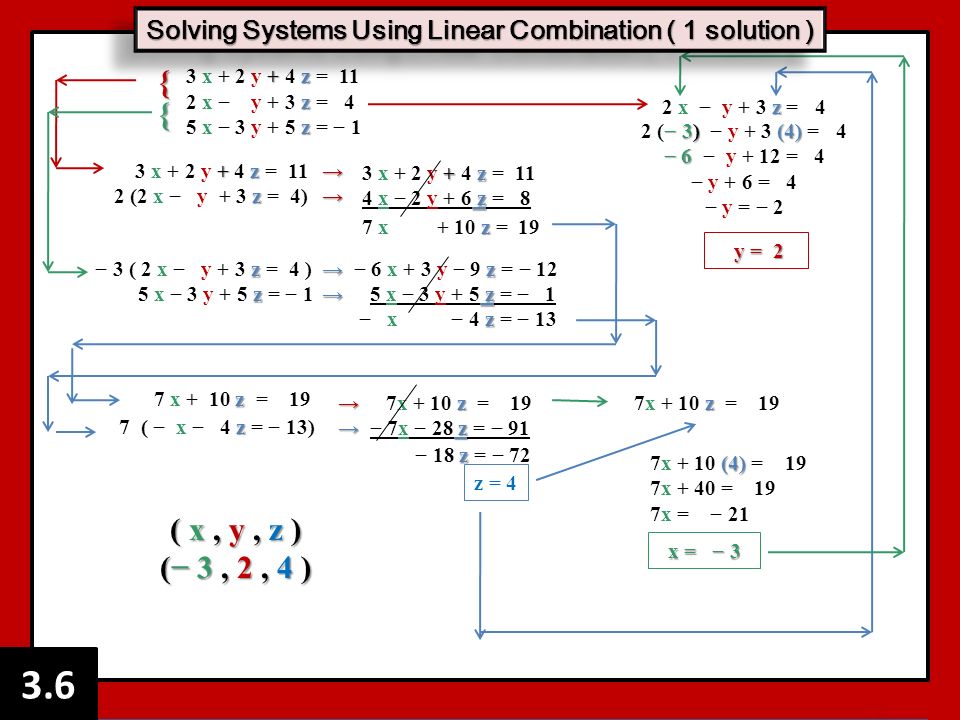


Algebra 2 Chapter 3 Notes Systems Of Linear Equalities And Inequalities Algebra 2 Chapter 3 Notes Systems Of Linear Equalities And Inequalities Ppt Download



Solved Finding An Equation Of A Tangent Plane In Exercise Chegg Com



Ma2e01 Tutorial Solutions 9 1 2 F


Using Matrix Method Solve The System Of Equations 3x 2y 2z 3 X 2y 3z 6 2x Y Z 2 Studyrankersonline



Misc 16 Solve Equations 2 X 3 Y 10 Z 4 4 X 6 Y 5 Z 1



0 件のコメント:
コメントを投稿